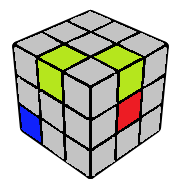
Pre-setup
After CP-line, we aim to get the left centre on the right face; and the LF and LB edges that make up the 1x2x3 block, in the top layer. One strategy to do this is to first get the centre to the right face using r and u moves, then bring one of the two edges to the top layer using r moves (or occasionally u and R moves), then place this edge in UL using U moves and finally bring the other edge to the top layer using r moves (or occasionally u and R moves).
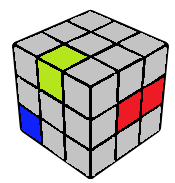
Setup
One of the 1x2x3 edges is to be attached to the centre. This can usually be done simply using a U move, or it may require first placing an edge in UF and doing u' R u. It needs to be ensured that at the end of this substep the centre should remain in the right face, and the remaining edge should remain in the upper layer. The attached edge can be moved out of the U layer using an R move to enable the remaining edge to move freely in the U layer.
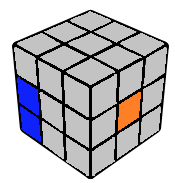
Extension
The remaining edge now is connected the centre opposite to the first edge. This can sometimes be done using only R and U moves, though sometimes it may be required to place the connected edge in BR and the remaining edge in UF and doing u' R u; this depends on the orientation of the remaining edge. Following this, the extension can be attached to the line in DL using an appropriate R move and a u2. This completes a 1x2x3 block on left.

pEO
Now, we need to ensure that the DB edge is correctly oriented, while placing either the U or the D centre in the U face. If an F or B centre is in the top face, bring a misoriented edge in UB using R and U moves, and do an r move; else bring an oriented edge to UF and do an r2 move (which is better than checking the orientation of DB and taking action accordingly). In this process, one may attempt to preserve good edges by pushing them out of the M slice.