YruRU

Locate 5 and 6

The DBL corner is assumed to be solved by definition, and this defines the orientation of the cube. If the DFL corner is solved as well, we say that the DL corners are solved; in this case we simply need to locate where corners 5 and 6 (for this particular orientation). If the DFL corner is not permuted correctly (i.e. some other corner numbered X is in its spot) then we assume that the DFL corner (which will be in the U or R layers) is numbered X and continue by locating corners 5 and 6 in this modified numbering system.

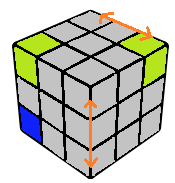
Mental Swaps

We always want 5 and 6 to be friends as defined in the numbering system section. If 5 and 6 are not friends, we visualise two pairs of corners as swapped such that 5 and 6 become friends while keeping the CP case the same. The first swap is always done between "6" and "the friend of 5", so that now 5 and 6 are friends. There are two cases for the second swap. If 5 and 6 initially have the same parity (as in the above picture), we mentally swap the third corner with the same parity with the friend of 6. Else, if 5 and 6 have different parity, then we mentally swap the third pair of friends (i.e. the pair of friends that neither 5 nor 6 is a part of) with each other.

Reading the Thread

Once we have mentally swapped the required pieces, we look at the parity of 5. If 5 is in an odd position, we read the corners in the order UFL-UBL-UBR-UFR-DFR-DBR; else if 5 is in an even position, we read the corners in the opposite direction. The "thread" along which the corners have to be read is highlighted in orange in the figure above. Reading the thread will give us a permutation of the numbers from 1 to 6. We simply need to ignore the numbers 5 and 6, thus we now have a permutations of the numbers 1, 2, 3 and 4.

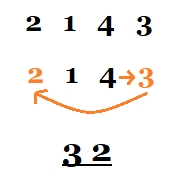
Detemining the CP case

The sequence of 4 numbers obtained in the last substep now has to be converted to an ordered pair of two distinct numbers out of 1, 2 aand 3. This is done by first locating the number 4 in the sequence, and then listing out the cyclically following numbers. An example is given in the image above. There are 6 possible ordered pairs we can remain with, each corresponding to a CP case (for example, 12 indicates solved CP). Given this ordered pair of numbers, we can determine how to solve CP as indicated in the text below

Once the CP case has been identified, the CP can be solved by swapping a pair of corners. Here is the list of corners that can be swapped in each CP case. Note, any one of the three possible swaps can be done to solve the CP. The ways to perform these swaps are in the execution sections.

CP Case	Option 1	Option 2	Option 3	Comments
12	Nil	Nil	Nil	This corresponds to solved CP, no swaps required
13	2 - 3	1 - 6	4 - 5
21	1 - 2	3 - 5	4 - 6	This corresponds to a diagonal swap on the R face
23	1 - 4	2 - 5	3 - 6	All options have a difference of 3
31	3 - 4	1 - 5	2 - 6
32	1 - 3	2 - 4	5 - 6	This corresponds to a diagonal swap on the U face

A pnemonic device to memorise swaps with 1 in this order are "Absorb an acid along arm." The length of each word is the corner that 1 swaps with in that case. A pnemonic device to memorise swaps with 4 in this order are "Quite strong, I can be." The length of each word is the corner that 4 swaps with in that case. Given that no pair appears twice in the table and the pattern in the case of the "23" CP case, One should be able to recreate the table. This will become automatic over time.

While this way of detemining which corners to swap to solve CP seems too elaborate to be worth it, the advanced way of handling this can allow CP recognition in under 3 seconds with little practice. Also, this is quite complicated to follow at first, so it is recommended to take aid of example solves.