YruRU

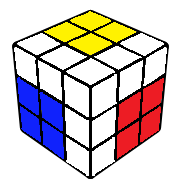
EO-CP-2x2x3

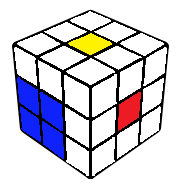
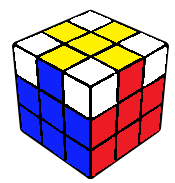
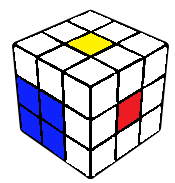
This is where one is expected to end up after successfully doing the first three steps. With the R and U layers remaining, edges oriented and corners permuted, the rest of the cube can be solved using only R and U moves.

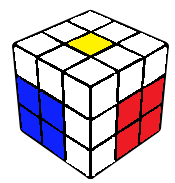
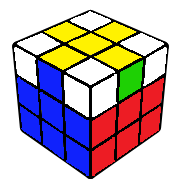
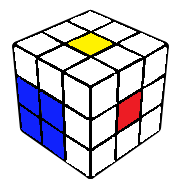
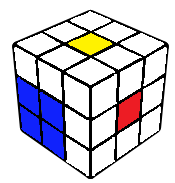
Square on top

A 2x2x1 block is constructed on the top layers. This can be done by connecting one edge with the top centre, followed by the solving of a corner-edge pair. The edge can usually be connected such that we get an easy corner-edge pair case.

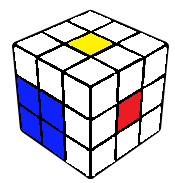
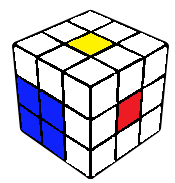
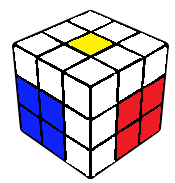
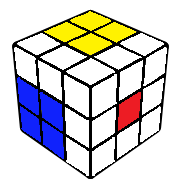
F2L

The final corner edge pair is solved, typically intuitively. However, this can also be broken down into 20 cases. This is less than the typical CFOP last slot since EO is already done. The algorithms for each case can be found in the F2L algorithms section.

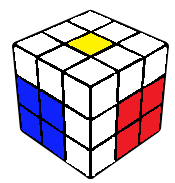
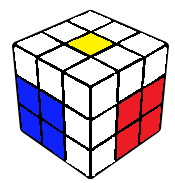
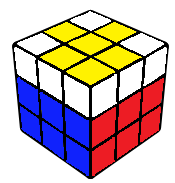
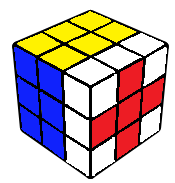
2GLL

The last layer is now the right layer, which can be finished using one of 84 2GLL algorithms after doing a z' rotation. The solve can also be continued in one of the following ways, however after doing a z' rotation.

EO-CP-2x2x3

Square

A 2x2x1 block is constructed on the first two layers. This can be done by connecting one edge with the right centre, followed by the solving of a corner-edge pair. The edge can usually be connected such that we get an easy corner-edge pair case.

OLS

The last pair is solved while orienting the top layer corners. This can usually be done by winter variation, summer variation, or some other 2-gen set. This is however only suitable if an EPLL skip is certain, or if the OLS case is extremely easy.

EPLL

The solve needs to be finished using one of four O-2GLL cases, or edge PLLs. These are generally much quicker to recognise and execute, and one in twelve times this step gives a skip is OLS is done at random.

EO-CP-2x2x3

Square

Unphasing

The final corner-edge pair is solved, while ensuring that the edges in the final layer are unphased, i.e. edges that are supposed to opposite are placed adjacent to each other. This requires active correction once every three solves, by slightly modifying the insertion.

2GLL

The last layer is solved using one of 56 2GLL algorithms. These algorithms are shorter in general and easier to recognise, since they cannot contain cases such as pure twists, etc. However, the possibility of an LL skip goes from 1/324 to zero if applied blindly.

EO-CP-2x2x3

Square

Phasing

The final corner-edge pair is solved, while ensuring that the edges in the final layer are unphased, i.e. edges that are supposed to opposite are placed opposite to each other. This requires active correction twice every three solves, by slightly modifying the insertion.

2GLL

The last layer is solved using one of 28 2GLL algorithms. These algorithms are longer in general although much easier to recognise due to the reduction in cases. The possibility of an LL skip goes from 1/324 to 1/108 on application.

EO-CP-2x2x3

Square

Suning (Soon-ing)

The final corner-edge pair is solved, while ensuring that the OCLL case is either sune, antisune, or solved; i.e. exactly one or all corners. This requires active correction twice every three solves, by slightly modifying the insertion.

2GLL

The last layer is solved using one of 28 2GLL cases. These cases on average are over two shorter than the average 2GLL cases and are much easier to recognise. The possibility of an LL skip goes from 1/324 to 1/108 on application.

EO-CP-2x2x3

Psuedo-Square

A 2x2x1 block is constructed on the first two layers, but is an R2 away from being solved. This is usually done when such a square is preserved after EOBF, or is only one move away from forming, with no other obvious blocks available.

Psuedo-F2L

The right block is completed by adding the final corner-edge pair, such that the entire 1x2x3 block is an R2 away from being solved. Certain OLS such as winter variation are especially useful in such situations to aid recognition of following steps.

2GLL

The last layer is solved using a 2GLL algorithm followed by an R2 to finish. The 2GLL can be identified by inverting the colours on pieces that have the bottom colour. EPLLs are considerably easier to recognise compared to other 2GLLs, making OLS or even 2LLL worth it.

EO-CP-2x2x3

First Square

A 2x2x1 block is constructed on one of the two layers. This can be done by connecting one edge with the right centre, followed by the solving of a corner-edge pair. The edge can usually be connected such that we get an easy corner-edge pair case.

Second Square

Another 2x2x1 block is constructed on another layer using similar techniques. This may be worth it when the second square is already formed or one move from being formed, and the corner-edge pair continuation of the first square is not great.

Finish

The final few pieces are solved using a subset of the tripod or the snake algorithm set. The recognition of this set can be tricky and thus this route is worth it only in extreme cases. Most algortihms however are quite efficient and fast.

Most of these methods are likely not substantially better than simple square > F2L > 2GLL; however a sensibly chosen combination of the above techniques across (or even within) solves on a case-by-case basis can provide a substantial boost of efficiency. The major benefit of having a CP-first approach rather than simply doing right block followed by ZBLL (other than a much lower algorithm count and faster recognition of course), is the extreme amounts of freedom one has in the 2-gen finish; applying many of the above techniques may even be impractical in the latter style of solving. Appropriate use of this freedom can lead to great solves.

That said, it is important to note that we already know that the entire upcoming solve is going to be 2-gen, thus keeping it clean and simple while giving TPS the priority will be key in most solves.