YruRU

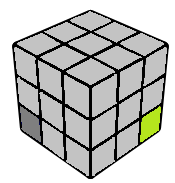
Corner "1"

As long as the bottom colour is yellow, this corner will be numbered "1" irrespective of the orientation along Y axis.

Corner "2"

As long as the bottom colour is yellow, this corner will be numbered "2" irrespective of the orientation along Y axis.

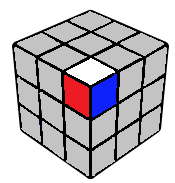
Corner "3"

As long as the bottom colour is yellow, this corner will be numbered "3" irrespective of the orientation along Y axis.

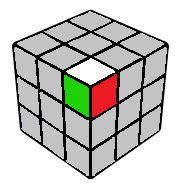
Corner "4"

As long as the bottom colour is yellow, this corner will be numbered "4" irrespective of the orientation along Y axis.

Corner "5"

The corner that belongs in DFR when the line is held in DL will be numbered "5". This depends on the orientation of the line along Y axis and can change from solve to solve despite having yellow bottom.

Corner "6"

The corner that belongs in DBR when the line is held in DL will be numbered "6". This depends on the orientation of the line along Y axis and can change from solve to solve despite having yellow bottom.

Position Parity

The pink positions in the above image are called odd positions and the blue positions in the above image are called even positions. The line is supposed to be in DL; and there are 3 positions of each parity.

Friends

There are three pairs of friends in the 6 remaining corners given the line is held in DL, as shown in the image above. The friend pairs are UFL-UBL, UBR-UFR and DFR-DBR.

Average movecount: 4 - 5

Average double moves: ~ 1

Algorithms: 0

This is the basic numbering system that one will require to know to understand the beginner and advanced corner tracing. The idea is to identify the CP case using this numbering system, and make a 1x1x3 block in DL while solving the CP case. Each case will be solved by "swapping" a pair of corners.

A similar numbering of corners from 1 to 4 can be done on the yellow face as well if you wish to be x2 neutral; however the numbering must be clockwise for left-handed OH solvers. It may be tempting to be x2 y neutral (i.e. have 8 possible starts), however it is strongly recommended to be x2 y2 neutral (i.e. have only 4 possible starts) since this speeds up all four steps in the method to varying degrees.