Algorithmic methods are doing fairly well compared to block building methods, and for good reason. TPS on the new hardware has shot up and it makes sense to make best use of it. Here is a part of a spreadsheet by Brest analysing the World Championship 2019 3x3x3 Finals containing the average STPS of the 14 CFOP solvers during First 2 Layers (F2L) and Last Layer (LL). Despite there being OLL-recognition and PLL-recognition pauses, the average (algorithmic) LL turning speed for these solvers is on average 1 STPS faster than their (intuitive/semi-intuitive) F2L turning speed. For notable solvers like Tymon and Feliks, this difference is over 3 STPS.
Motivated by this premise, a method with a bearable number of algorithms, yet highly algorithmically reliant and with good recognition and algorithms has the potential to beat a good deal of methods. A means to achieve that is to have 3 algorithmic steps (compared to 2 for CFOP for example); while ensuring that those algorithms do indeed tackle a large set of cases (2LLL CFOP handles ~62k cases, so the said algorithms should handle 62k^(3/2) ~ 15M cases). The about page dives into the details of how such a method was derived.
While an algorithmic method promises high turning speed, it usually has the disadvantage of having a high movecount to go along. For example, order of the big-3 by fraction solved intuitively is Roux > ZZ > CFOP, while the order of these methods by movecount in STM is Roux < ZZ < CFOP. But, interestingly, the movecount of (human) Mehta is comparable to (human) Roux (stats and simulation results can be found in the variants' sections). These are in a nutshell what make this method a compelling candidate to at least compete with the big-3.
Movecount: 45-50
Algorithms: 130 - 843

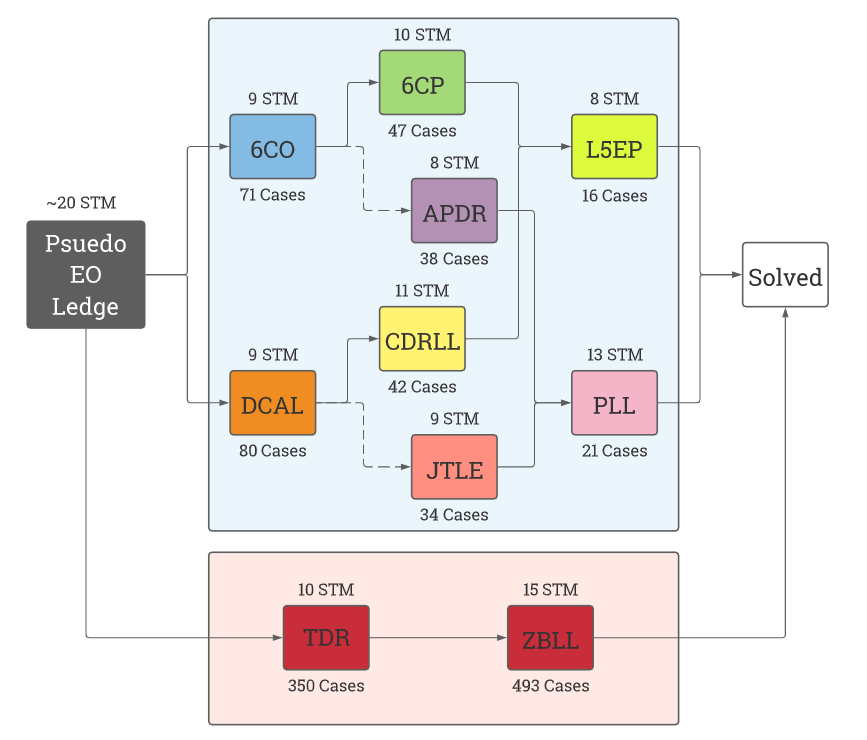
The above is a flowchart that depicts the entire Mehta family of methods. [Note that this flowchart may not accurately incorporate the AUFs needed to do between steps, thus simply adding average movecounts along each path will not necessarily give the precise movecount for that path.]
The first step is to solve a pseudo-EO-Ledge (also called simply EO-ledge henceforth). An EO-ledge is when a 1x2x3 block is solved on DL (specifically the D centre, the DF, DL and DB edges, and the DFL and DBL corners), the E layer belt is solved (though not necessarily aligned with the 1x2x3 block, hence the prefix "pseudo"), and the remaining 5 edges (the 4 U layer edges and the DR edge) are oriented. Solved traditionally (First block + 3-quarters belt + EO-last-edge), it takes 18-21 moves during a colour-neutral speedsolve. A much more detailed explanation of this step is given in the EO-ledge section.
From this point, there are two variations of the method.
Many other variants are possible for this method, and a great deal of them have been tested for recognition, algortihm-length and execution; of these, the OS system and the TDR variant are far superior compared to the rest.
The method can be extended to big cubes as is done in Mehta-MH. It can also be applied to puzzles like Square-1, 2x2x2, etc. However the effectiveness compared to the currently popular methods is unknown.